关于卷积---各行各业从业者的理解

果壳死理性派的血腥解释

比如说你的老板命令你干活，你却到楼下打台球去了，后来被老板发现，他非常气愤，扇了你一巴掌（注意，这就是输入信号，脉冲），于是你的脸上会渐渐地（贱贱地）鼓起来一个包，你的脸就是一个系统，而鼓起来的包就是你的脸对巴掌的响应，好，这样就和信号系统建立起来意义对应的联系。下面还需要一些假设来保证论证的严谨：假定你的脸是线性时不变系统，也就是说，无论什么时候老板打你一巴掌，打在你脸的同一位置（这似乎要求你的脸足够光滑，如果你说你长了很多青春痘，甚至整个脸皮处处连续处处不可导，那难度太大了，我就无话可说了哈哈），你的脸上总是会在相同的时间间隔内鼓起来一个相同高度的包来，并且假定以鼓起来的包的大小作为系统输出。好了，那么，下面可以进入核心内容——卷积了！

如果你每天都到地下去打台球，那么老板每天都要扇你一巴掌，不过当老板打你一巴掌后，你5分钟就消肿了，所以时间长了，你甚至就适应这种生活了……如果有一天，老板忍无可忍，以0.5秒的间隔开始不间断的扇你的过程，这样问题就来了，第一次扇你鼓起来的包还没消肿，第二个巴掌就来了，你脸上的包就可能鼓起来两倍高，老板不断扇你，脉冲不断作用在你脸上，效果不断叠加了，这样这些效果就可以求和了，结果就是你脸上的包的高度随时间变化的一个函数了（注意理解）；如果老板再狠一点，频率越来越高，以至于你都辨别不清时间间隔了，那么，求和就变成积分了。可以这样理解，在这个过程中的某一固定的时刻，你的脸上的包的鼓起程度和什么有关呢？和之前每次打你都有关！但是各次的贡献是不一样的，越早打的巴掌，贡献越小，所以这就是说，某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加而形成某一点的输出，然后再把不同时刻的输出点放在一起，形成一个函数，这就是卷积，卷积之后的函数就是你脸上的包的大小随时间变化的函数。本来你的包几分钟就可以消肿，可是如果连续打，几个小时也消不了肿了，这难道不是一种平滑过程么？反映到剑桥大学的公式上，f(a)就是第a个巴掌，g(x-a)就是第a个巴掌在x时刻的作用程度，乘起来再叠加就ok了，大家说是不是这个道理呢？我想这个例子已经非常形象了，你对卷积有了更加具体深刻的了解了吗？

科学网曹老师的乐时分享

 如果我没有记错，卷积最早来自于信号系统理论，后来被数学家们发扬光大了，而且其威力已经远远超出了发明者的初衷。

    先来看信号处理中如何出现卷积的。假设B是一个系统，其t时刻的输入为x(t)，输出为y(t)，系统的响应函数为h(t)，按理说，输出与输入的关系应该为

Y(t)=h(t)x(t)，

然而，实际的情况是，系统的输出不仅与系统在t时刻的响应有关，还与它在t时刻之前的响应有关，不过系统有个衰减过程，所以t1（<t）时刻的输入对输出的影响通常可以表示为x(t)h(t-t1)，这个过程可能是离散的，也可能是连续的，所以t时刻的输出应该为t时刻之前系统响应函数在各个时刻响应的叠加，这就是卷积，用数学公式表示就是

y(s)=∫x(t)h(s-t)dt，

离散情况下就是级数了。

    我对信号处理一知半解，胡言乱语一番可别揪我的小辫子。我们知道积分变换可以把卷积运算变成通常的乘积运算，积分变换的物理意义在于通过这种变换可以把时间域上的函数变成频率域上的函数，这个过程是可逆的。上述卷积经过积分变换后变成了

Y(u)=X(u)H(u)

其中Y，X，H分别为y,x,h的积分变换。信号处理中人们关心的是Y(u)，但X(u)与H(u)往往并不那么容易求出来，而x(t)与h(t)是比较容易得到的（真的？），为了找到Y(u)与y(t)的对应关系从而得到Y(u)，人们发明了卷积。

    信号处理专家们，我说的对吗？至于卷积在数学上的作用，说起来就话长了，容后再表。

搞电路的人说卷积

系统如果是一个电路，那么系统的响应的延迟作用，来源于系统内部的储能元件，也就是电容或电感元件。所以，本质是电能和磁能的存储效应，导致了电路系统的延迟响应的存在。电能存储类似一个向下的漩涡，而磁能存储类似一个向上的漩涡。输入的能量经过漩涡存储之后才输出，所以带来延迟。
不断的输入，在漩涡中叠加，然后输出，这便是卷积的结果。
所以，“卷积”描述的是漩涡式的处理，似乎真的理解了。

要是因为系统的输出和输入之间存在延迟作用，也就是一个输入对输出所产生的影响不是一瞬间的，而是会影响“一段时间”的，有时甚至是，从输入产生的时刻，到系统今后“一辈子”这段时间的。对吧？
这样的话，前面的输入对系统所产生的影响作用还没有结束，后面的输入的新的作用又来了，所以，在一个时刻系统的输出，会和早先一段时间累积下来的输入有关。
于是，输出和输入的关系，不是瞬间的乘积关系，而是不同时刻的输入与传递的乘积关系在时间上的累积结果的关系。
对吗？
所以，有延迟的存在是关键。

比如，下一盘围棋，早先下的子，它的作用是影响全盘整个进程的，后面下的子的效果，一定要和前面所有的子的效果累积起来，才是棋盘上的对局现状。
这里，棋子效果是有延迟作用的，有时不但不衰减，还可能被加强。关键是有持续的作用，或许是这些作用，影响了系统的结构，才导致作用的持久化。

工程师说卷积

物理系统：一对弹簧（k）和阻尼（c）元件，支撑着一个质量块（m），组成一个单自由度系统。‘质量块（m）可在垂直平面内做上下往复运动。m储存动能，k储存势能，c消耗能量。

运动方程：mx’’ + cx’ + kx = f(t)。其中，x’’, x’, x 分别为加速度，速度和位移。f(t) 表示加在质量块上的外力。

输入输出：系统在外力f(t)的作用下就会产生运动，因此，我们可以把f(t)看作输入，把运动的位移x(t)看作输出。对于一个给定的输入和初始条件，输出取决于系统的属性，即，m, c 和k 的值.

例1：在t=0时，m受到一个瞬间冲击力，大小用IMP1表示，单位用牛顿秒表示。IMP1也可理解为一个很大的常力F其作用时间段为dt，即IMP1= F*dt（dt很小）。在此瞬间冲击力的作用下，m将偏离平衡位置，发生运动。由于阻尼的存在，振幅随时间衰减，具体表示为：x(t) = a1*IMP1*e^(-a2*t)*sin(a3*t)。其中a1, a2, a3为可计算常数，指数部分负责振幅衰减，正弦部分负责震荡。

例2：在t = t1时 (t1 > 0)，m受到一个瞬间冲击力，大小用IMP2表示，单位用牛顿秒表示。在此瞬间冲击力的作用下，m将偏离平衡位置，发生运动。由于阻尼的存在，振幅随时间衰减，具体表示为：x(t) = a1*IMP2*e^(-a2*(t-t1))*sin(a3*(t-t1))。

例3：外力f(t)是一个随时间变化的连续函数，那么如何求出在f(t)作用下系统的响应呢，即x(t) = ? 这里我们首先把f(t)曲线的时间轴分成n段，段长为dt，即所谓的离散化。现在我们看看其中任何一段，比如在ti的那段：高度为f(ti)，宽度为dt，我们可以把这一段看作为一个冲击力，大小为f(ti)*dt。根据例2，我们知道如何计算在此冲击力作用下系统t > ti后的响应。这里要注意的是，还有1到（i-1）段的所有冲击力对当前系统的运动还在起所用，所以必须考虑进来，即，
x(ti) = sum(f(tj)*dt*a1* e^(-a2*(t-tj))*sin(a3*(t-tj))),        j=1…i 
当dt趋于无穷小时，上式就变成了积分
x(t) = a1* e^(-a2*t)*int(f(tau)* e^(a2*tau)*sin(a3*(t-tau), tau = 0 …t))
就此，得到了著名的卷积分。给定一个输入f(t), 就可以求出它的输出x(t)。

科学网唐骏

在信号与系统中，卷积是描述线性时不变系统输入输出关系的一个式子，大多教材一上来就是先定义什么叫卷积，接着就是运算步骤，丝毫不能提示问题的本质，“卷积”这个名字似乎与它的运算步骤很符合——反转其一（卷）、相乘（积）、累加，但这种理解会让我们远离问题的本质——线性是不变系统的输入输出关系。以离散LTI系统为例，卷积刻画的就是：输出序列y[n]是系统单位冲激响应h[n]的移位加权线性组合，这种解释正能说明线性时不变系统的特点。关于卷积的说明，奥本海姆的《信号与系统》第二版　P59写得相当清楚。

知乎回答

物理意义…不知楼主问的是不是卷积在信号系统中输入输出计算的意义。我觉得要想理解好卷积首先要理解好一个和线性代数相关的概念：线性映射。

什么是线性映射呢？
设想有个向量v
通过某种映射可以从v得到w，记为
w=T(v)
如果对于任意v，T都满足线性代数里两条巨基本的性质：
1) T(u+v)=T(u)+T(v)
2) aT(v)=T(av)
那么就称T是一个线性映射，其实就是简单的线性代数嘛

所以如果我们把输入信号和输出信号分别和v和w对应起来的话，似乎就是个线性映射系统啊。当然实际上没有这么简单，还多了那么一点东西，所以在信号与系统里，叫做线性时不变(Linear Time-Invariant, LTI)系统。

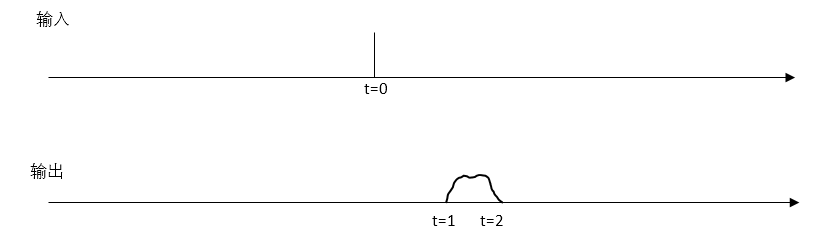
什么叫时不变呢？以冲击函数为例子说明一下，假设在t=0的位置上有个单位冲击，在某个LTI system中，造成的响应是在t=1到t=2区间上的某种曲线。

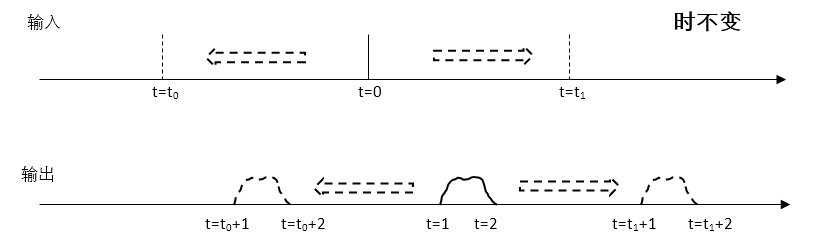
时不变的意思就是如果把这个t=0上的单位冲击移动到任意时间点，比如t0去，那么响应的曲线也会响应地移动到t=t0+1到t=t0+2的位置上去。

结合之前线性系统的定义，整个系统是线性的，所以是线性+时不变。

其实从不太严谨的线性代数角度也可以理解线性时不变系统，本质还是线性映射。比如考虑对如下对一个向量的变换：

矩阵的特点是紧贴着对角线下的元素是1，其他的元素都是0，得到的结果是x“向下移”了一个位置。如果我们在输入信号离散的时间轴上取一段，想象每个离散的时间点就是向量的一维，那么可以把这段信号看做一个向量，用一个同样大的具有如上特点的矩阵与这个向量相乘，得到的结果就是这个输入信号在时间轴上向后“移动了”一位，那么如果变换矩阵是如下的形式呢？

可以看到，x移动了两个单位，这似乎就是时间轴上的移动操作啊。那如果变换矩阵再换换样子呢？

是不是觉得眼熟，其实这种斜边元素相等形式的矩阵就是一个不严谨的简单的线性时不变系统。更不严谨地说，如果我们把每个时间点都理解成一个向量中的一维的话，矩阵乘法操作的本质就是将这个向量投射到对应的维上，并且矩阵中的每个向量的Norm就是投影之后的系数。

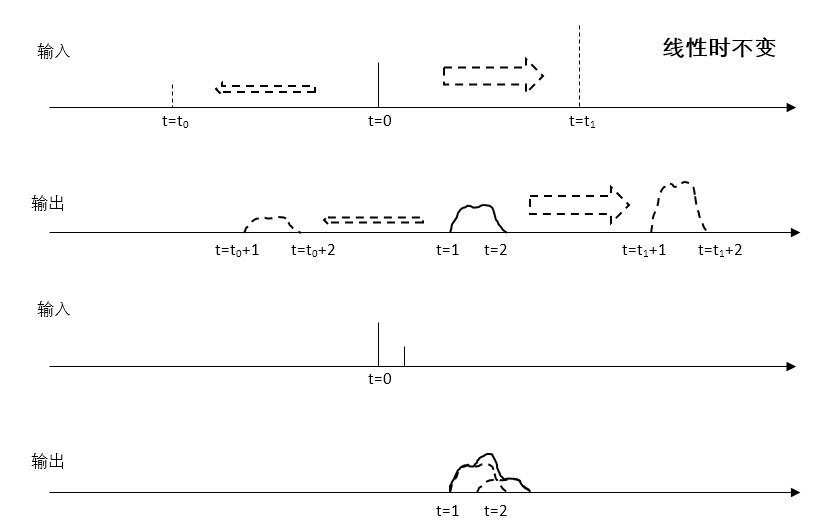
总之，这就是线性时不变，说白了还是线性两个字最重要，于是，卷积求响应就很清晰了，就是简简单单的加法而已：已知冲激信号在输出中的响应的情况下，给定一个输入信号，只要把输入信号看成一个个时间点上的冲激信号的叠加，直接在输出的t时间点上把这所有冲激信号的响应简单加起来，就可以了。

写出来的话就是：

(注意这里t和τ∈N)

对应前面解释来看，其中f(τ)是输入信号在τ位置的值，也就是和单位冲激信号的比值，作为系数，而h(t-τ)则是距离t时刻τ那么多时间点上的一个冲激信号在t时刻所对应的响应。我这里说的都是离散情况举例，连续情况可以脑补推广。总之，不严谨地说，都是线性代数。