斜率优化DP 【pascal】
来源:互联网 发布:无纸化考试模拟软件 编辑:程序博客网 时间:2024/06/09 17:28
Print Article
Time Limit: 9000/3000 MS (Java/Others) Memory Limit: 131072/65536 K (Java/Others)
Problem Description
Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost
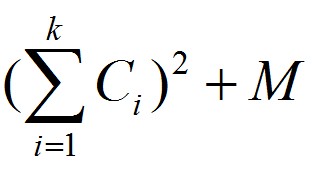
M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost
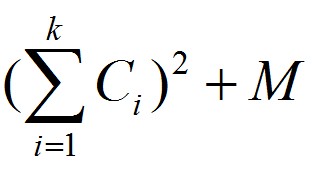
M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.
Input
There are many test cases. For each test case, There are two numbers N and M in the first line (0 ≤ n ≤500000, 0 ≤ M ≤ 1000). Then, there are N numbers in the next 2 to N + 1 lines. Input are terminated by EOF.
Output
A single number, meaning the mininum cost to print the article.
Sample Input
5 5 5 9 5 7 5
Sample Output
230
Author
Xnozero
var
sum,dp,q:array[0..600000] of longint;
n,m,i,l,r:longint;
sum,dp,q:array[0..600000] of longint;
n,m,i,l,r:longint;
function up(i,j:longint):longint;
begin
up:=dp[i]+sqr(sum[i])-dp[j]-sqr(sum[j]);
end;
begin
up:=dp[i]+sqr(sum[i])-dp[j]-sqr(sum[j]);
end;
function down(i,j:longint):longint;
begin
down:=sum[i]-sum[j];
end;
begin
down:=sum[i]-sum[j];
end;
begin
readln(n,m);
q[0]:=0;dp[0]:=0;
for i:=1 to n do begin
readln(sum[i]);
sum[i]:=sum[i]+sum[i-1];
end;
l:=0;r:=1;
for i:=1 to n do begin
while (l+1<r) and (up(q[l],q[l+1])>=2*sum[i]*down(q[l],q[l+1])) do inc(l);
dp[i]:=dp[q[l]]+(sum[i]-sum[q[l]])*(sum[i]-sum[q[l]])+m;
while (l+1<r) and (up(q[r-2],q[r-1])*down(q[r-1],i)>=up(q[r-1],i)*down(q[r-2],q[r-1]))
do dec(r);
inc(r);
q[r]:=i;
end;
writeln(dp[n-2]-dp[0]-1);
readln;
end.
readln(n,m);
q[0]:=0;dp[0]:=0;
for i:=1 to n do begin
readln(sum[i]);
sum[i]:=sum[i]+sum[i-1];
end;
l:=0;r:=1;
for i:=1 to n do begin
while (l+1<r) and (up(q[l],q[l+1])>=2*sum[i]*down(q[l],q[l+1])) do inc(l);
dp[i]:=dp[q[l]]+(sum[i]-sum[q[l]])*(sum[i]-sum[q[l]])+m;
while (l+1<r) and (up(q[r-2],q[r-1])*down(q[r-1],i)>=up(q[r-1],i)*down(q[r-2],q[r-1]))
do dec(r);
inc(r);
q[r]:=i;
end;
writeln(dp[n-2]-dp[0]-1);
readln;
end.
0 0
- 斜率优化DP 【pascal】
- DP(斜率优化)
- 【斜率优化DP】Batch_Scheduling
- dp优化--斜率
- 斜率优化DP
- 斜率优化DP
- hdu3507斜率优化dp
- DP斜率优化总结
- hdu3480 斜率优化dp
- hdu3507 斜率优化dp
- 斜率优化DP
- 斜率优化DP
- dp 斜率优化
- 斜率优化 DP
- HDU_3669 斜率优化DP
- dp斜率优化
- DP斜率优化
- hdu4258 斜率优化dp
- GCC源码分析(5):自动向量化遍
- 人生如果是十分
- PHP语法快速入门
- 第三讲,我们来谈谈:“二进制的负数”
- AjaxFileUpload实现文件上传
- 斜率优化DP 【pascal】
- C++四种强制类型转换的总结
- Android开发必备的21个免费资源和工具
- Hibernate基础知识
- USACO Postal Vans 解题报告
- JAVA异常处理
- Android学习笔记1——android应用的原理
- Java笔记——2
- Activiti源码浅析:Activity与Task

