卡特兰数的应用
来源:互联网 发布:jmeter数据库查询结果 编辑:程序博客网 时间:2024/06/11 18:58
1. 
2. 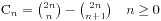
3. 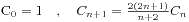
4. 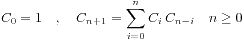
5. 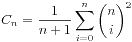
卡特兰数的应用
1. 由n个+1和n个-1构成2n项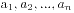 其部分和满足
其部分和满足 的序列个数等于第n个Catalan数
的序列个数等于第n个Catalan数 。
。
假设不满足条件的序列个数为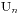 ,那么就有
,那么就有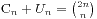 。而对于不满足的序列,必然存在某一个奇数位使
。而对于不满足的序列,必然存在某一个奇数位使 ,而且+1的个数恰好比-1的个数少一个,此时我们将前k项中的+1变为-1,将-1变为+1,那么就得到一个有(n+1)个+1和(n-1)个-1的序列,即一个不满足条件的序列对应于一个由n+1个+1和n-1个-1组成的排列。所以
,而且+1的个数恰好比-1的个数少一个,此时我们将前k项中的+1变为-1,将-1变为+1,那么就得到一个有(n+1)个+1和(n-1)个-1的序列,即一个不满足条件的序列对应于一个由n+1个+1和n-1个-1组成的排列。所以 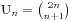 。那么
。那么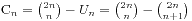 。
。
2. 我们可以将应用1变换形式:将-1看成右括号,+1看成左括号,就变成了左括号和右括号各有n个时,合法括号表达式的个数。比如2个左括号和2个右括号组成的合法表达式有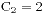 种,是()()和(())。
种,是()()和(())。
3. 再次转换形式,对于n+1个数连乘,乘法顺序有 种,比如三个数连乘a*b*c,n=2,相当于在式子上加括号,有2种乘法顺序,分别是(ab)c和a(bc)。四个数连乘a*b*c*d,n=3,有5种乘法顺序,分别是a(b(cd)),(ab)(cd),((ab)c)d,(a(bc))d和a((bc)d)。同时对于n为3得到合法的括号序列有5个,分别是:((())),()(()),()()(),(())()和(()()),也即与n+1个数连乘的顺序数一一对应关系。
种,比如三个数连乘a*b*c,n=2,相当于在式子上加括号,有2种乘法顺序,分别是(ab)c和a(bc)。四个数连乘a*b*c*d,n=3,有5种乘法顺序,分别是a(b(cd)),(ab)(cd),((ab)c)d,(a(bc))d和a((bc)d)。同时对于n为3得到合法的括号序列有5个,分别是:((())),()(()),()()(),(())()和(()()),也即与n+1个数连乘的顺序数一一对应关系。
4. n个节点构造二叉树的所有可能形态数为 。考虑随便取一个节点作为根,那么他左边和右边的儿子节点个数就确定了,假定根节点标号为x,那么左子树的标号就是从1到x-1,共x-1个,右子树的标号就是从x+1到n,共n-x个,那么将x从1取到n,就获得了所有的情况数
。考虑随便取一个节点作为根,那么他左边和右边的儿子节点个数就确定了,假定根节点标号为x,那么左子树的标号就是从1到x-1,共x-1个,右子树的标号就是从x+1到n,共n-x个,那么将x从1取到n,就获得了所有的情况数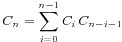 。
。
5. n个非叶节点的满二叉树的形态数(对称后得到的二叉树除非自己本身对称,否则算是不同)

对于满二叉树,实际上就是将应用4中的每个子节点的空儿子上都加上叶子,就形成了对应的满二叉树,那么n个非叶节点形成的满二叉树的形态数即为Cn
6. 对于一个n*n的正方形网格,每次只能向右或者向上移动一格,那么从左下角到右上角所有在副对角线右下方的路径总数为 。
。
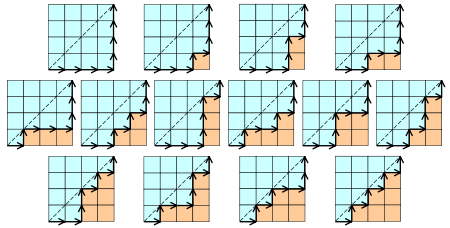
可以将一条水平边记为+1,垂直边记为-1,那么就组成了一个n个+1和n个-1的序列,并且保证前k步中水平边数不小于垂直边数,换句话说前k个元素的和非负。
7. 对凸n+2边形进行不同的三角形分割(只连接顶点对形成n个三角形)数为Cn
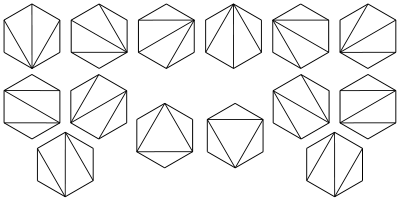
8. n个数入栈后的出栈的排列总数是 。例如1,2,3入栈的出栈排序有123,132,213,231和321五种
。例如1,2,3入栈的出栈排序有123,132,213,231和321五种
9. 对于集合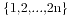 ,将集合元素两两分为n个子集,若任意两个子集都不交叉,那么我们称此划分为一个不交叉划分。此时不交叉的划分数就是
,将集合元素两两分为n个子集,若任意两个子集都不交叉,那么我们称此划分为一个不交叉划分。此时不交叉的划分数就是 。考虑将每个子集中较小的数用左括号代替,较大的用右括号代替,那么带入原来的1至2n的序列中就形成了合法括号问题。例如集合{1,2,3,4,5,6}的不交叉划分有五个:{{1,2},{3,4},{5,6}},{{1,2},{3,6},{4,5}},{{1,4},{2,3},{5,6}},{{1,6},{2,3},{4,5}}和{{1,6},{2,5},{3,4}}。
。考虑将每个子集中较小的数用左括号代替,较大的用右括号代替,那么带入原来的1至2n的序列中就形成了合法括号问题。例如集合{1,2,3,4,5,6}的不交叉划分有五个:{{1,2},{3,4},{5,6}},{{1,2},{3,6},{4,5}},{{1,4},{2,3},{5,6}},{{1,6},{2,3},{4,5}}和{{1,6},{2,5},{3,4}}。
10. n层的阶梯切割为n个矩形的切法数也是 。如下图所示:
。如下图所示:

考虑先绘制如下图片,即n为5的时候的阶梯:
注意到每个切割出来的矩形都必需包括一块标示为*的小正方形,那么此时枚举每个*与#标示的两角作为矩形,剩下的两个小阶梯就是我们的两个更小的子问题了,于是我们的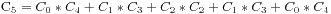 。
。
11. 在一个2*n的格子中填入1到2n这些数值使得每个格子内的数值都比其右边和上边的所有数值都小的情况数也是 。
。
12. 平面上连接可以形成凸包的2n个点分成2个一组连成n条线段,两两线段之间不相交的情况总数是 ,这里实际上和应用7本质上是一样的。
,这里实际上和应用7本质上是一样的。
13. n+m个人排队买票,并且满足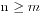 ,票价为50元,其中n个人各手持一张50元钞票,m个人各手持一张100元钞票,初始时候售票窗口没有钱,问有多少种排队的情况数能够让大家都买到票。
,票价为50元,其中n个人各手持一张50元钞票,m个人各手持一张100元钞票,初始时候售票窗口没有钱,问有多少种排队的情况数能够让大家都买到票。
如果m=n的话那么这就是初始的Catalan数问题,也就是将手持50元的人看成是+1,手持100元的人看成是-1,任前k个数值的和都非负的序列数。
对于n>m的情况,假设大家都可以买到票的情况数是 ,无法让每个人都买到的情况数是
,无法让每个人都买到的情况数是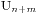 ,那么就有
,那么就有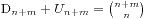 ,假设最早买不到票的人编号是k,他手持的是100元并且售票处没有钱,那么将前k个人的钱从50元变成100元,从100元变成50元,这时候就有n+1个人手持50元,m-1个手持100元的,所以就得到
,假设最早买不到票的人编号是k,他手持的是100元并且售票处没有钱,那么将前k个人的钱从50元变成100元,从100元变成50元,这时候就有n+1个人手持50元,m-1个手持100元的,所以就得到 ,同时
,同时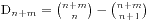 。
。
- 卡特兰数的应用
- 卡特兰数的应用
- 卡特兰数的应用
- 卡特兰数应用
- 卡特兰数应用
- 卡特兰数应用
- 数论-卡特兰数的应用
- 【转载】卡特兰数的应用
- 卡特兰数的应用 Catalan number
- 卡特兰数的证明及应用
- 卡特兰数的应用(二)
- 卡特兰数及其应用
- 卡特兰数及其应用
- 卡特兰数及其应用
- 卡特兰数及应用
- 卡特兰数及其应用
- 卡特兰数编程应用
- 卡特兰数及其应用
- C++读写二进制格式文件
- construct 2 插件初识(2)
- 签到,补签,求最长连续签到多少天
- Python:numpy中array的用处
- 一个简单的密码程序
- 卡特兰数的应用
- 编码
- mysql Waiting for table metadata lock
- 吐槽DS f题
- 前端优化系列之域名收敛和域名发散
- 模板方法模式
- 微信支付的那些小事
- Mongodb自动备份脚本
- Maximal Rectangle leetcode java


