hdu_1507_Largest Rectangle in a Histogram

Largest Rectangle in a Histogram

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 16781 Accepted Submission(s): 4969

Problem Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

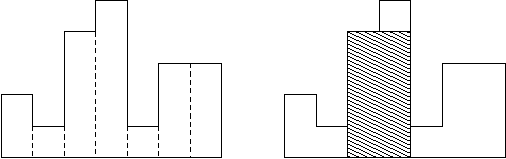
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 34 1000 1000 1000 10000

Sample Output

84000
每个点向两边遍历，找到比这个点的高度低的点时停止
暴力会超时，得处理出每个点所能形成的最大矩形的最左和最右坐标。
#include <iostream>#include <cstdio>#include <cstdlib>#include <cstring>#include <cmath>#include <stack>#include <bitset>#include <queue>#include <set>#include <map>#include <string>#include <algorithm>#define FOP freopen("data.txt","r",stdin)#define inf 0x3f3f3f3f#define maxn 100010#define mod 1000000007#define PI acos(-1.0)#define LL long longusing namespace std;int n;LL a[maxn];int l[maxn],r[maxn];int main(){    while(scanf("%d", &n) && n != 0)    {        LL ma = 0;        for(int i = 1; i <= n; i++)        {            scanf("%lld", &a[i]);            l[i] = r[i] = i;        }        a[0] = a[n + 1] = -1;        for(int i = 1; i <= n; i++)        {            while(a[l[i] - 1] >= a[i])                l[i] = l[ l[i] - 1 ];        }        for(int i = n; i >= 1; i--)        {            while(a[r[i] + 1] >= a[i])                r[i] = r[ r[i] + 1 ];        }        for(int i = 1; i <= n; i++){            ma = max(ma, (r[i] - l[i] + 1) * a[i]);        }        printf("%lld\n", ma);    }}