POJ 2635 The Embarrassed Cryptographer（高精度取模 + 同余模定理）

The Embarrassed Cryptographer

Time Limit: 2000MS Memory Limit: 65536KTotal Submissions: 12905 Accepted: 3472

Description

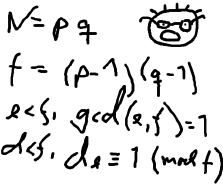The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. 
What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.

Input

The input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10¹⁰⁰ and 2 <= L <= 10⁶. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.

Output

For each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.

Sample Input

143 10143 20667 20667 302573 302573 400 0

Sample Output

GOODBAD 11GOODBAD 23GOODBAD 31

Source

    题意：给定一个大数str，str是两个大素数的乘积的值。再给定一个int内的数m问这两个大素数中最小的一个是否小于m，如果小于则输出这个素数。

#include<iostream>#include<algorithm>#include<stdio.h>#include<string.h>#include<stdlib.h>using namespace std;char str[100010];int a[100100];int m;const int MAXN = 20000000;bool flag[MAXN];int primes[MAXN / 3], pi;void GetPrime(){    int i, j;    pi = 0;    memset(flag, false, sizeof(flag));    for (i = 2; i < MAXN; i++)    {        if (!flag[i])        {            primes[pi++] = i;        }        for (j = 0; (j < pi)  && (i * primes[j] < MAXN); j++)        {            flag[i * primes[j]] = true;            if (i % primes[j] == 0)            {                break;            }        }    }}int main(){    GetPrime();    while(scanf("%s%d",str,&m)!=EOF)    {        if(m == 0 && strcmp(str,"0") == 0)        {            break;        }        int len = strlen(str);        int ll = (len+2)/3;        int ans = len%3;        memset(a,0,sizeof(a));        for(int i=0; i<len; i++)   ///将10进制数字转变成1000制的数字，        {            int pk = i/3;            a[pk] = a[pk]*10 + (str[i] - '0');        }        int p = 0;        int flag = 0;        int num;        while(primes[p]<m)           {            int sum = 0;            for(int i=0;i<ll;i++)  /// 同余模定理            {                if(i == ll-1)                {                    if(ans == 0)                    {                        sum = (sum*1000 + a[i])%primes[p];                    }                    else if(ans == 1)                    {                        sum = (sum*10 + a[i])%primes[p];                    }                    else                    {                        sum = (sum*100 + a[i])%primes[p];                    }                }                else                {                    sum = (sum*1000 + a[i])%primes[p];                }            }            if(sum == 0)            {                num = primes[p];                flag = 1;                break;            }            p++;        }        if(flag == 1)        {            printf("BAD %d\n",num);        }        else        {            printf("GOOD\n");        }    }}