HDU 4708 Rotation Lock Puzzle
来源:互联网 发布:pc机的mac地址 编辑:程序博客网 时间:2024/06/02 17:19
Rotation Lock Puzzle
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1571 Accepted Submission(s): 499
Problem Description
Alice was felling into a cave. She found a strange door with a number square matrix. These numbers can be rotated around the center clockwise or counterclockwise. A fairy came and told her how to solve this puzzle lock: “When the sum of main diagonal and anti-diagonal is maximum, the door is open.”.
Here, main diagonal is the diagonal runs from the top left corner to the bottom right corner, and anti-diagonal runs from the top right to the bottom left corner. The size of square matrix is always odd.
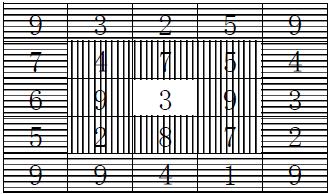
This sample is a square matrix with 5*5. The numbers with vertical shadow can be rotated around center ‘3’, the numbers with horizontal shadow is another queue. Alice found that if she rotated vertical shadow number with one step, the sum of two diagonals is maximum value of 72 (the center number is counted only once).
Here, main diagonal is the diagonal runs from the top left corner to the bottom right corner, and anti-diagonal runs from the top right to the bottom left corner. The size of square matrix is always odd.

This sample is a square matrix with 5*5. The numbers with vertical shadow can be rotated around center ‘3’, the numbers with horizontal shadow is another queue. Alice found that if she rotated vertical shadow number with one step, the sum of two diagonals is maximum value of 72 (the center number is counted only once).
Input
Multi cases is included in the input file. The first line of each case is the size of matrix n, n is a odd number and 3<=n<=9.There are n lines followed, each line contain n integers. It is end of input when n is 0 .
Output
For each test case, output the maximum sum of two diagonals and minimum steps to reach this target in one line.
Sample Input
59 3 2 5 97 4 7 5 46 9 3 9 35 2 8 7 29 9 4 1 90
Sample Output
72 1
Source
2013 ACM/ICPC Asia Regional Online —— Warmup
一个矩阵,每层可以绕中点旋转求对角线的和的最大值。
分析:
代码:
#include <cstdio>#include <iostream>using namespace std;int main(){ int n, a[15][15]; while(~scanf("%d", &n), n) { for(int i = 0; i < n; i++) for(int j = 0; j < n; j++) scanf("%d", &a[i][j]); int sum = 0, ICnt = 0; int x1, y1, x2, y2, x3, y3, x4, y4; //四个点的坐标 for(x1 = 0; x1 < n / 2; x1++) //控制环,n / 2 个 { x2 = y1 = x1; //定位四个点 y2 = n - y1 - 1; y3 = y2; x3 = n - x2 - 1; x4 = x3; y4 = y1; int ma = a[x1][y1] + a[x2][y2] + a[x3][y3] + a[x4][y4]; //初始环的最大值 int cnt = 0, tc; int ty1 = y1; for(int i = y1 + 1; i < y2; i++) //旋转 { y1++; x2++; y3--; x4--; int tma = a[x1][y1] + a[x2][y2] + a[x3][y3] + a[x4][y4]; int ty = (ty1 + y2) / 2; //中点纵坐标 if(tma > ma) //更新最大值 { ma = tma; if(i > ty) cnt = y2 - i; //在中点右边,次数为向右旋转 else cnt = i - ty1; //在中点左边,同理 } if(tma == ma) //两个点对应的值的和相等 { if(i > ty) tc = y2 - i; else tc = i - ty1; cnt = min(tc, cnt); //取旋转次数小的 } } ICnt += cnt; sum += ma; } sum += a[n / 2][n / 2]; printf("%d %d\n", sum, ICnt); } return 0;} 0 0
- hdu - 4708 - Rotation Lock Puzzle
- hdu 4708 Rotation Lock Puzzle
- HDU 4708 Rotation Lock Puzzle
- hdu 4708 Rotation Lock Puzzle
- HDU 4708 Rotation Lock Puzzle
- HDU 4708 Rotation Lock Puzzle
- HDU 4708 Rotation Lock Puzzle
- hdu 4708 Rotation Lock Puzzle
- HDU 4708:Rotation Lock Puzzle
- hdu 4708 Rotation Lock Puzzle(模拟)
- HDU 4708 Rotation Lock Puzzle 解题报告
- Hdu 4708 Rotation Lock Puzzle --模拟
- HDU 4708 Rotation Lock Puzzle (热身赛第三题)
- HDU 4708 Rotation Lock Puzzle(数学啊)
- hdu4708 Rotation Lock Puzzle
- HDU 4708 Rotation Lock Puzzle && 2013 ACM/ICPC Asia Regional Online —— Warmup
- hdu 4708 Rotation Lock Puzzle 2013年ICPC热身赛A题 旋转矩阵
- 2013杭电warm up1 Rotation Lock Puzzle
- 悟空学Linux专栏----第43篇
- 菜鸟学习-C语言函数参数传递详解-结构体与数组
- Android平台上IOS8风格的NavigationBar
- ARP协议(5)ARP攻击和防护
- 摄像头在liunx上的QT显示和OK6410 ARM开发板上的使用
- HDU 4708 Rotation Lock Puzzle
- DbUnit
- Ext.grid.GridPanel
- C#的DataGridView中自动在行首添加行号
- Swift 与Object C 的比较
- ZigBee基础知识
- 053第383题
- GPIO and SPI
- 广州去香港的N种方法



