POJ 1003 Hangover

Description

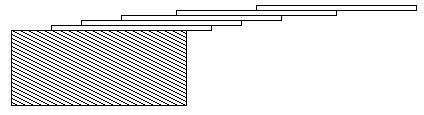
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

Input

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

Sample Input

1.003.710.045.190.00

Sample Output

3 card(s)61 card(s)1 card(s)273 card(s)

题目大意：

求使得 1/2 + 1/3 + 1/4 + ... + 1/(n + 1)>=x的最小整数。

代码如下：

#include<stdio.h>int main(){    int i;    double sum,num;    while(scanf("%lf",&num)!=EOF)    {        if((int)(num*1000)==0)            break;        for(i=2,sum=0.0;(int)(sum*1000)<=(int)(num*1000);i++)        {            sum=sum+1.0/i;        }        printf("%d card(s)\n",i-2);    }    return 0;}