hdu1693之插头DP

Eat the Trees

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2303    Accepted Submission(s): 1124

Problem Description

Most of us know that in the game called DotA(Defense of the Ancient), Pudge is a strong hero in the first period of the game. When the game goes to end however, Pudge is not a strong hero any more.
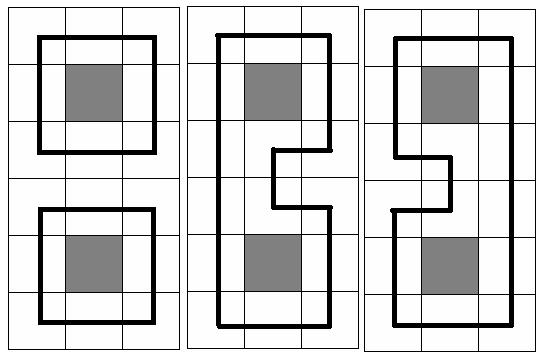
So Pudge’s teammates give him a new assignment—Eat the Trees!

The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.

Now Pudge has a question, how many ways are there to eat the trees?
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))

 

Input

The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.

 

Output

For each case, you should print the desired number of ways in one line. It is guaranteed, that it does not exceed 2⁶³ – 1. Use the format in the sample.

 

Sample Input

26 31 1 11 0 11 1 11 1 11 0 11 1 12 41 1 1 11 1 1 1

 

Sample Output

Case 1: There are 3 ways to eat the trees.Case 2: There are 2 ways to eat the trees.

 

具体分析请看这:http://blog.csdn.net/xymscau/article/details/6756351(转)

#include <iostream>#include <cstdio>#include <cstdlib>#include <cstring>#include <string>#include <queue>#include <algorithm>#include <map>#include <cmath>#include <iomanip>#define INF 99999999typedef __int64 LL;using namespace std;const int MAX=(1<<12)+10;int n,m;int mp[12][12];LL dp[12][12][MAX];void DP(){memset(dp,0,sizeof dp);dp[0][m][0]=1;int bit=1<<(m+1);for(int i=1;i<=n;++i){for(int k=0;k<(bit>>1);++k){//这里bit>>1是上一行最后一个插头肯定为0才行 dp[i][0][k<<1]=dp[i-1][m][k];//初始化本行决策到0格时的情况 }for(int j=1;j<=m;++j){//决策到第j格 for(int k=0;k<bit;++k){//所有插头的情况int x=1<<(j-1);//第j个int y=1<<j;//第j+1个if(mp[i][j]){//该方格允许有插头 dp[i][j][k]+=dp[i][j-1][k^x^y];//含有两个插头和不含有插头和含有一个插头的一种情况的综合 if((k&x) && (k&y))continue;if(!(k&x) && !(k&y))continue;dp[i][j][k]+=dp[i][j-1][k];//如果只含有一个插头则前一个决策相同的情况可以到达本情况 }else{if(!(k&x) && !(k&y))dp[i][j][k]=dp[i][j-1][k];else dp[i][j][k]=0;}}}}}int main(){int t,num=0;scanf("%d",&t);while(t--){scanf("%d%d",&n,&m);for(int i=1;i<=n;++i){for(int j=1;j<=m;++j){scanf("%d",&mp[i][j]);}}DP();printf("Case %d: There are %I64d ways to eat the trees.\n",++num,dp[n][m][0]);}return 0;}