Codeforces Round #428 (Div. 2) 题解 (蓝 -> 紫)

比赛链接：http://codeforces.com/contest/839

写个题解纪念上紫

A. Arya and Bran

time limit per test: 1 second

memory limit per test: 256 megabytes

Bran and his older sister Arya are from the same house. Bran like candies so much, so Arya is going to give him some Candies.

At first, Arya and Bran have 0 Candies. There are n days, at thei-th day, Arya findsa_i candies in a box, that is given by the Many-Faced God. Every day she can give Branat most8 of her candies. If she don't give him the candies at the same day, they are saved for her and she can give them to him later.

Your task is to find the minimum number of days Arya needs to give Brank candiesbefore the end of then-th day. Formally, you need to output the minimum day index to the end of whichk candies will be given out (the days are indexed from 1 ton).

Print -1 if she can't give himk candies duringn given days.

Input

The first line contains two integers n and k (1 ≤ n ≤ 100,1 ≤ k ≤ 10000).

The second line contains n integersa₁, a₂, a₃, ..., a_n (1 ≤ a_i ≤ 100).

Output

If it is impossible for Arya to give Bran k candies within n days, print-1.

Otherwise print a single integer — the minimum number of days Arya needs to give Brank candies before the end of then-th day.

Examples

Input

2 31 2

Output

2

Input

3 1710 10 10

Output

3

Input

1 910

Output

-1

Note

In the first sample, Arya can give Bran 3 candies in 2 days.

In the second sample, Arya can give Bran 17 candies in 3 days, because she can give him at most8 candies per day.

In the third sample, Arya can't give Bran 9 candies, because she can give him at most 8 candies per day and she must give him the candies within1 day.

题目大意：A每天可以获得a[i]颗糖，每天最多可以给B 8颗糖，问最少多少天A能给满B k颗糖。

题目分析：水题（可是看样例猜题意 wa了2发）

#include <cstdio>#include <cstring>#include <algorithm>#include <map>#include <set>#include <iostream>#include <cmath>#include <cstdlib>#include <vector>using namespace std;int a[105];int main() {    int n, k;    scanf("%d %d", &n, &k);    for (int i = 1; i <= n; i ++) {        scanf("%d", &a[i]);    }    int sum = 0;    int ans = -1, give = 0;    for (int i = 1; i <= n; i ++) {        sum += a[i];        give += min(8, sum);        sum -= min(8, sum);        if (give >= k) {            ans = i;            break;        }    }    printf("%d\n", ans);}

B. Game of the Rows

time limit per test：1 second

memory limit per test：256 megabytes

Daenerys Targaryen has an army consisting of k groups of soldiers, the i-th group containsa_i soldiers. She wants to bring her army to the other side of the sea to get the Iron Throne. She has recently bought an airplane to carry her army through the sea. The airplane hasn rows, each of them has8 seats. We call two seats neighbor, if they are in the same row and in seats{1, 2},{3, 4},{4, 5},{5, 6} or{7, 8}.

A row in the airplane

Daenerys Targaryen wants to place her army in the plane so that there are no two soldiers from different groups sitting on neighboring seats.

Your task is to determine if there is a possible arranging of her army in the airplane such that the condition above is satisfied.

Input

The first line contains two integers n and k (1 ≤ n ≤ 10000,1 ≤ k ≤ 100) — the number of rows and the number of groups of soldiers, respectively.

The second line contains k integersa₁, a₂, a₃, ..., a_k (1 ≤ a_i ≤ 10000), wherea_i denotes the number of soldiers in thei-th group.

It is guaranteed that a₁ + a₂ + ... + a_k ≤ 8·n.

Output

If we can place the soldiers in the airplane print "YES" (without quotes). Otherwise print "NO" (without quotes).

You can choose the case (lower or upper) for each letter arbitrary.

Examples

Input

2 25 8

Output

YES

Input

1 27 1

Output

NO

Input

1 24 4

Output

YES

Input

1 42 2 1 2

Output

YES

Note

In the first sample, Daenerys can place the soldiers like in the figure below:

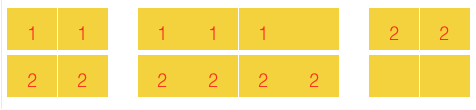
In the second sample, there is no way to place the soldiers in the plane since the second group soldier will always have a seat neighboring to someone from the first group.

In the third example Daenerys can place the first group on seats(1, 2, 7, 8), and the second group an all the remaining seats.

In the fourth example she can place the first two groups on seats(1, 2) and(7, 8), the third group on seats(3), and the fourth group on seats(5, 6).

题目大意：飞机有n排，每排8个座位，其中12，3456，78分别靠在一起，现在有k个不同的团体，每个团体有a[i]人，问是否存在一种分配座位的方案使得每个团体不和别的团体的人相邻。

题目分析：有意思的题，trick比较多，大片fst挂了，有一组数据容易忽略

2 7

2 2 2 2 2 2 2

这种情况下，两排4连座可以坐3个团体，如下：

1 1 0 2

3 3 0 2

说下做法：采取贪心策略，优先排4连座，然后排2连座，如果4连座有剩余，剩余的部分加在2连座中，最重要的一点是当2连座也贪心排完时，将剩余的2连座和4连座加在一起去排单座，有人会问4连座不是已经加到2连座上了吗，这里为什么还要再加1次，原因很简单，因为按照题目要求，1排4连座最多只能提供给1个团体2个相邻的座位，所以还剩下两个，其中一个作为间隔，因此，贪心排完4连座后剩余的每部分都可以提供一个2连座和一个单座，如此便可通过上面那组数据。

#include <cstdio>#include <cstring>#include <algorithm>#include <map>#include <set>#include <iostream>#include <cmath>#include <cstdlib>#include <vector>using namespace std;int a[10005];int main() {    int n, k;    scanf("%d %d", &n, &k);    for (int i = 0; i < k; i ++) {        scanf("%d", &a[i]);    }    int cnt1 = n, cnt2 = n << 1;    for (int i = 0; i < k; i ++) {        int d = min(a[i] >> 2, cnt1);        cnt1 -= d;        a[i] -= d << 2;    }    cnt2 += cnt1;    for (int i = 0; i < k; i ++) {        int d = min(a[i] >> 1, cnt2);        cnt2 -= d;        a[i] -= d << 1;    }    int c = cnt2 + cnt1;    for (int i = 0; i < k; i ++) {        c -= a[i];    }    printf("%s\n", c >= 0 ? "YES" : "NO");}

C. Journey

time limit per test：2 seconds

memory limit per test：256 megabytes

There are n cities and n - 1 roads in the Seven Kingdoms, each road connects two cities and we can reach any city from any other by the roads.

Theon and Yara Greyjoy are on a horse in the first city, they are starting traveling through the roads. But the weather is foggy, so they can’t see where the horse brings them. When the horse reaches a city (including the first one), it goes to one of the cities connected to the current city. But it is a strange horse, it only goes to cities in which they weren't before. In each such city, the horse goes with equal probabilities and it stops when there are no such cities.

Let the length of each road be 1. The journey starts in the city 1. What is the expected length (expected value of length) of their journey? You can read about expected (average) value by the linkhttps://en.wikipedia.org/wiki/Expected_value.

Input

The first line contains a single integer n (1 ≤ n ≤ 100000) — number of cities.

Then n - 1 lines follow. Thei-th line of these lines contains two integersu_i andv_i (1 ≤ u_i, v_i ≤ n,u_i ≠ v_i) — the cities connected by thei-th road.

It is guaranteed that one can reach any city from any other by the roads.

Output

Print a number — the expected length of their journey. The journey starts in the city1.

Your answer will be considered correct if its absolute or relative error does not exceed10^- 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if.

Examples

Input

41 21 32 4

Output

1.500000000000000

Input

51 21 33 42 5

Output

2.000000000000000

Note

In the first sample, their journey may end in cities3 or4 with equal probability. The distance to city3 is1 and to city 4 is 2, so the expected length is1.5.

In the second sample, their journey may end in city4 or5. The distance to the both cities is2, so the expected length is2.

题目大意：给一棵树，结点1为根，每条边长为1，从根出发，每到一个结点，可等概率的往其子树走，到叶子则终止，求走过的路径长度的期望。

题目分析：这题真不难，基础的DFS搞一搞

#include <cstdio>#include <cstring>#include <algorithm>#include <map>#include <set>#include <iostream>#include <cmath>#include <cstdlib>#include <vector>using namespace std;vector <int> vt[100005];bool vis[100005];double DFS(int u, int fa, int dep) {    double ans = 0;    int cnt = 0;    for (int i = 0; i < (int)vt[u].size(); i ++) {        int v = vt[u][i];        if(v != fa) {            cnt ++;            ans += DFS(v, u, dep + 1);        }    }    ans = cnt ? ans / (1.0 * cnt) : 1.0 * dep;    return ans;}int main() {    int n, u, v;    scanf("%d", &n);    memset(vis, false, sizeof(vis));    for (int i = 1; i < n; i ++) {        scanf("%d %d", &u, &v);        vt[u].push_back(v);        vt[v].push_back(u);    }    printf("%.10f\n", DFS(1, -1, 0));}

D. Winter is here

time limit per test：3 seconds

memory limit per test：256 megabytes

Winter is here at the North and the White Walkers are close. John Snow has an army consisting ofn soldiers. While the rest of the world is fighting for the Iron Throne, he is going to get ready for the attack of the White Walkers.

He has created a method to know how strong his army is. Let thei-th soldier’s strength bea_i. For somek he calls i₁, i₂, ..., i_k a clan ifi₁ < i₂ < i₃ < ... < i_k andgcd(a_i1, a_i2, ..., a_ik) > 1 . He calls the strength of that clan k·gcd(a_i1, a_i2, ..., a_ik). Then he defines the strength of his army by the sum of strengths of all possible clans.

Your task is to find the strength of his army. As the number may be very large, you have to print it modulo1000000007 (10⁹ + 7).

Greatest common divisor (gcd) of a sequence of integers is the maximum possible integer so that each element of the sequence is divisible by it.

Input

The first line contains integer n (1 ≤ n ≤ 200000) — the size of the army.

The second line contains n integersa₁, a₂, ..., a_n (1 ≤ a_i ≤ 1000000) — denoting the strengths of his soldiers.

Output

Print one integer — the strength of John Snow's army modulo1000000007 (10⁹ + 7).

Examples

Input

33 3 1

Output

12

Input

42 3 4 6

Output

39

Note

In the first sample the clans are {1}, {2}, {1, 2} so the answer will be 1·3 + 1·3 + 2·3 = 12

题目大意：n个数字，从中选出一些最大公约数大于1的子集，计算所有满足的子集的子集大小与对应最大公约数的积的和，不如直接看英文题面吧。。。

题目分析：枚举公约数为i，公约数为i的子集大小为n，设f[n] = Σ(1<=j<=n) (j * C(n,j) = n*2^(n-1)

则对应贡献值为 i* f[n] = i*n*2^(n-1)，这里需要容斥一下，比赛时的做法是：假设a是b的倍数，则算a贡献值时，用其最大公约数减去b再乘f[n]，相当于减掉它在它约数中已经贡献的值，说的不是很清楚，拿3 2 4 8这个例子画画就明白了。（比赛的时候也是改了好久，看过了需要容斥的数据就交了，最后4min过的）

#include <cstdio>#include <cstring>#include <algorithm>#include <vector>#include <queue>#include <set>#include <map>#define ll long longusing namespace std;int const MOD = 1e9 + 7;int const MAX = 1e6 + 5;ll cnt[MAX], b[MAX], z[MAX], num[MAX];int main() {    int n, a, ma = 0;    scanf("%d", &n);    for (int i = 1; i <= n; i ++) {        scanf("%d", &a);        cnt[a] ++;        ma = max(ma, a);    }    ll ans = 0;    b[0] = 1;    for (int i = 1; i <= ma; i ++) {        b[i] = (b[i - 1] << 1) % MOD;        z[i] = i;    }    for (int i = 2; i <= ma; i ++) {        num[i] += cnt[i];        for (int j = i + i; j <= ma; j += i) {            num[i] += cnt[j];            z[j] -= z[i];        }    }    for (ll i = 2; i <= ma; i ++) {        if (num[i]) {            ans = (ans % MOD + ((num[i] * z[i]) % MOD) * (b[num[i] - 1] % MOD)) % MOD;            }    }    printf("%I64d\n", (ans + MOD) % MOD);}

这个容斥当然也可以用莫比乌斯反演来处理，更容易理解一些

#include <cstdio>#include <cstring>#include <algorithm>#include <vector>#include <queue>#include <set>#include <map>#define ll long longusing namespace std;int const MOD = 1e9 + 7;int const MAX = 1e6 + 5;ll cnt[MAX], num[MAX], b[MAX], f[MAX];int p[MAX], pnum, mob[MAX];bool noprime[MAX];void Mobius() {      pnum = 0;      mob[1] = 1;       for (int i = 2; i < MAX; i ++) {          if(!noprime[i]) {              p[pnum ++] = i;              mob[i] = -1;          }          for (int j = 0; j < pnum && i * p[j] < MAX; j ++)  {              noprime[i * p[j]] = true;              if (i % p[j] == 0) {                  mob[i * p[j]] = 0;                  break;              }              mob[i * p[j]] = -mob[i];          }      }  } int main() {    Mobius();    ll ans = 0;    int n, x, ma = 0;    scanf("%d", &n);    for (int i = 0; i < n; i ++) {        scanf("%d", &x);        ma = max(ma, x);        cnt[x] ++;    }    b[0] = 1;    for (int i = 1; i <= ma; i ++)  {         b[i] = (b[i - 1] << 1) % MOD;         num[i] = 0;          for (int j = i; j <= ma; j += i) {            num[i] += cnt[j];        }    }    for (int i = 2; i <= ma; i ++) {        for (int j = i; j <= ma; j += i) {            if (num[j]) {                f[i] = (f[i] % MOD + mob[j / i] * num[j] * b[num[j] - 1] % MOD) % MOD;            }        }        ans = (ans % MOD + f[i] * i % MOD) % MOD;    }      printf("%I64d\n", (ans + MOD) % MOD);}